Tommaso Comparin

I worked on many aspects of the quantum many-body problem, related to both equilibrium and out-of-equilibrium quantum states, making use of theoretical and computational techniques. My broader interest is in statistical physics and numerical methods, especially Monte Carlo algorithms.
Below are some projects I worked on:

Spin-squeezing generation with quantum simulators

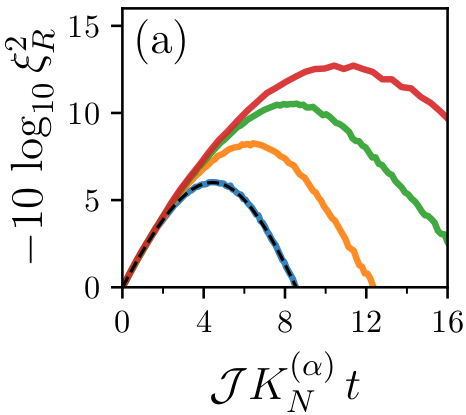Spin-squeezing dynamics Spin squeezing of the collective spin is a fundamental property of correlated quantum states, both as a resource for quantum metrology and as a witness of entanglement. The paradigmatic way to generate squeezing is the dynamics induced by the one-axis-twisting collective-spin dynamics (as realized e.g. with spinor Bose-Einstein condensates). We proposed two alternative strategies, suitable to a broad range of modern quantum-simulation platforms.
(1) Several platforms realize spin-1/2 models with slowly-decaying spin-spin couplings - e.g. Rydberg atoms with dipolar couplings, or trapped ions. For these systems, a quench protocol initialized in a coherent spin state generates spin squeezing at short time, where the dynamics remains close to the sector with maximal total spin. For couplings that are sufficiently long-range, the optimal squeezing value (obtained at finite time) has the same scaling properties as for the one-axis-twisting model - a consequence of the large overlap of the initial state with the so-called Anderson tower of states.
(2) For platform that realize short-range spin-1/2 models (like bosonic/fermionic Mott insulators in optical lattices, or superconducting circuits), we propose an alternative protocol for scalable spin squeezing. This consists in preparing a fully polarized ground state by means of a strong magnetic field, and then slowly reducing the field in the presence of spin-spin couplings. As the ground state tends to develop long-range order, transverse-spin fluctuations are reduced and the squeezing diverges (in the thermodynamic limit) as the fields tends to zero.

See:
  • T. Comparin, F. Mezzacapo, T. Roscilde, Multipartite entangled states in dipolar quantum simulators, Phys. Rev. Lett. 129, 150503 (2022) [arXiv:2205.03910]. Related data: 10.5281/zenodo.6534223.
  • T. Comparin, F. Mezzacapo, M. Robert-de-Saint-Vincent, T. Roscilde, Scalable spin squeezing from spontaneous breaking of a continuous symmetry, Phys. Rev. Lett. 129, 113201 (2022) [arXiv:2202.08607].
  • T. Comparin, F. Mezzacapo, T. Roscilde, Robust spin squeezing from the tower of states of U(1)-symmetric spin Hamiltonians, Phys. Rev. A 105, 022625 (2022) [arXiv:2103.07354]. Data and additional simulation details: 10.5281/zenodo.5993008.
  • T. Roscilde, F. Mezzacapo, T. Comparin, Spin squeezing from bilinear spin-spin interactions: two simple theorems, Phys. Rev. A 104, L040601 (2021) [arXiv:2106.07460].

    • Anyonic statistics in Fractional Quantum Hall states

    Moore-Read density profile Anyons are quantum indistinguishable objects which are neither bosons nor fermions, but have an intermediate statistics. This property is encoded in the phase acquired by the wave function upon the exchange of two particles. Solid-state physics is the main playground for studying anyons, which typically appear as excitations on top of a fractional quantum Hall state. More recently, ultracold atomic gases are seen as an alternative possibility for producing and detecting this kind of states.
    In our work, we propose a protocol to identify anyonic statistics in an ultracold-atoms setup, based on currently available experimental techniques. We make use of a general mathematical relation between angular momentum and the statistical phase to highlight the anyonic properties of quasihole excitations in fractional quantum Hall fluids. This protocol requires the knowledge of quantities as simple as the spatial size of the fluid at rest, or the density-depletion profile induced by a quasihole.
    We verify the validity of our approach in two paradigmatic cases, namely for the Laughlin and Moore-Read wave functions, by making use of the Monte Carlo sampling technique. In [Umucalilar, 2018] we demonstrate that we can correctly retrieve the braiding phase of Laughlin quasihole states, while in [Macaluso, 2019] we generalize our approach to the case of the non-Abelian anyonic excitations of the Moore-Read state. In the latter case, we are able to identify the different fusion channels of this anyonic model.
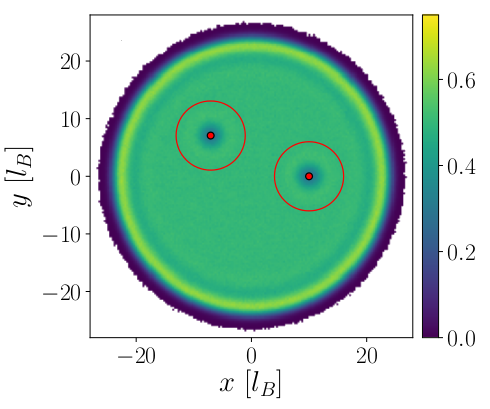
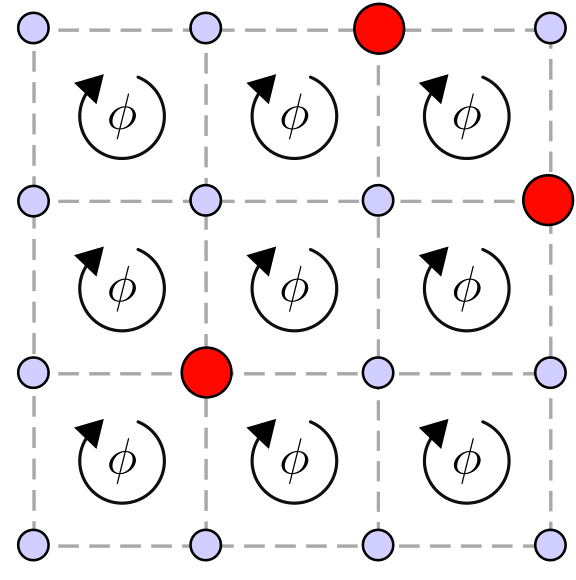    Harper-Hofstadter model After studying these Fractional Quantum Hall states, we focused on the corresponding states for lattice systems - known as Fractional Chern Insulators. We consider the Harper-Hofstadter model, a Bose-Hubbard model (see also Bose-Hubbard model in optical lattices) with complex hopping due to the presence of a gauge field. Already in the non-interacting case, complex hopping may induce non-trivial topological properties for the eigenstates of the system. This remains true for the case we consider, that is, in the presence of strong local interactions. As a method to identify the ground state, we make use of Tree Tensor Networks, which are a powerful variational Ansatz in the class of Tensor Network states (see for instance this review by Román Orús). For systems of up to 18 particles, we study the ground state in the presence of a harmonic trap. By adding some external pinning potentials, we generate and localize quasihole excitations with the expected fractional charge. We then apply the methods developed for the off-lattice Fractional Quantum Hall states to link the braiding phase of quasiholes to the depletion that they induce in the background density profile, and we observe a reasonable agreement with the expected results.

    See:
    • T. Comparin, A. Opler, E. Macaluso, A. Biella, A. P. Polychronakos, L. Mazza, Measurable fractional spin for quantum Hall quasiparticles on the disk, Phys. Rev. B 105, 085125 (2022) [arXiv:2111.02901]. Supporting data: 10.5281/zenodo.5734359.
    • E. Macaluso, T. Comparin, O. Umucalilar, M. Gerster, S. Montangero, M. Rizzi, I. Carusotto, Charge and statistics of lattice quasiholes from density measurements: a Tree Tensor Network study, Phys. Rev. Research 2, 013145 (2020) [arXiv:1910:05222].
    • E. Macaluso, T. Comparin, L. Mazza, I. Carusotto, Fusion channels of non-Abelian anyons from angular-momentum and density-profile measurements, Phys. Rev. Lett. 123, 266801 (2019) [arxiv:1903.03011].
    • R. O. Umucalilar, E. Macaluso, T. Comparin, I. Carusotto, Time-of-Flight Measurements as a Possible Method to Observe Anyonic Statistics, Phys. Rev. Lett. 120, 230403 (2018) [arxiv:1712.07940].
    • Scientific code associated to this project:
      T. Comparin, E. Macaluso. Laughlin-Metropolis [doi: 10.5281/zenodo.1193694].

      • Ultracold fermionic mixtures in two dimensions

      Dipolar equation of state The first experiments with ultracold gases made use of atoms with short-range interaction potentials. Other atoms (like Erbium and Dysprosium) have a larger dipole moment, and their interaction has a slow power-law decay at large interatomic distance. Ultracold gases of dipolar atoms are nowadays routinely produced in several labs, and were already employed to probe many-body features related to the peculiar dipole-dipole interaction potential.
      In [Comparin, 2019], we study a two-dimensional model for dipolar fermions at zero temperature by means of the quantum Monte Carlo technique. We focus on a binary mixture, namely a system of two fermionic components. We compute the energy and the pair distribution functions, and their dependence on the density. This constitutes a useful reference for future experiments in quasi-two-dimensional regimes.
      In the strongly-interacting regime, we address the possibility of itinerant ferromagnetism, that is, the situation where a single-species system has a lower energy than a mixture. The presence or absence of such feature depends on the interplay between fermionic statistics and strong repulsive interactions. In the case of dipoles in two-dimensions, the technical feat consists in computing ground-state energies with high accuracy, while still relying on the fixed-node approximation. In our study we make use of iterative-backflow trial wave functions within the quantum Monte Carlo approach, and observe no signature of a fully-polarized ground state.
      In [Bombín, 2019], we consider the extremely polarized system, where a single impurity is immersed in a fermionic bath. We compute the polaron energy and distribution functions via quantum Monte Carlo methods, and we determine observables related to the quasiparticle picture like the quasiparticle residue and the effective mass. We repeat the analysis for two models: one with dipolar interaction and one where the impurity interacts with an ideal Fermi bath through a hard-core potential.

      See:

      Unitary Bose gas

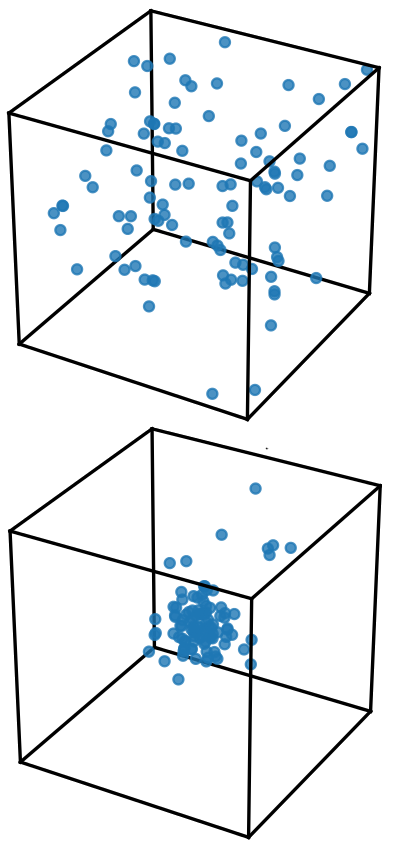      Efimov liquid The strength of interatomic interactions, in ultracold-atomic samples, can be tuned over a broad range through the Feshbach-resonance technique, from the weak-interactions limit to the unitary regime (where the scattering length diverges). This possibility is at the basis of the first experimental signature, in 2006, of Efimov trimer states, originally predicted in the 1970s in the nuclear-physics realm. In our work, we consider a many-body bosonic model with zero-range unitary interactions, and we use the path-integral quantum Monte Carlo technique to compute its properties. To better treat this model, the many-body algorithm is based on a direct-sampling scheme at the two-body level. The high-temperature phase is a normal gas, while at lower temperature the system exists in two different phases: The superfluid gas and the Efimov liquid. We compute the critical temperature for Bose-Einstein condensation and find that it is smaller than for the ideal Bose gas, by approximately 10%. We also determine the full momentum distribution of the gas, and compute Tan's contact parameter, which shows a non-monotonic dependence on temperature.

      See:
      • T. Comparin, W. Krauth. Momentum distribution in the unitary Bose gas from first principles, Phys. Rev. Lett. 117, 225301 (2016) [arXiv:1604.08870].
      • T. Comparin, From few-body atomic physics to many-body statistical physics: The unitary Bose gas and the three-body hard-core model (PhD thesis, 2016), pdf.

      Bose-Hubbard model in a BEC vortex lattice

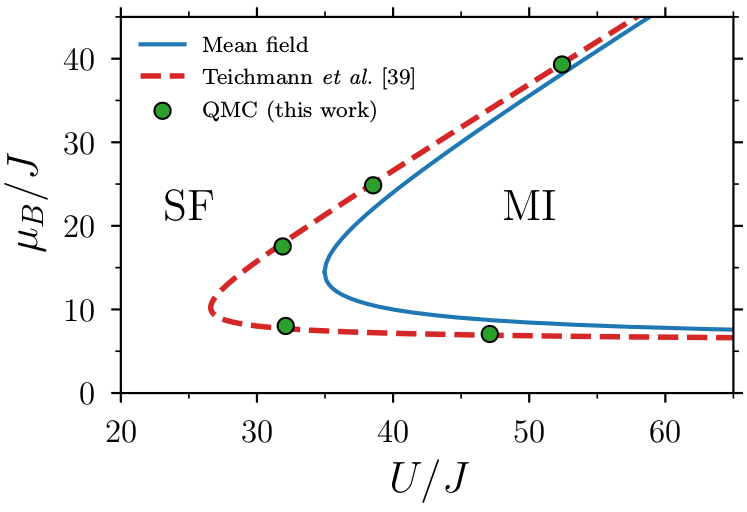      Bose-Hubbard model The appearance of a triangular lattice of vortices (the Abrikosov lattice) is a peculiar feature of superfluids and superconductors. In experiments with ultracold atoms under rotation, it was possible to observe the formation of this lattice, and to study its normal-mode excitations (the Tkachenko oscillations). In two papers together with researchers from the Instituto de Física de São Carlos and BEC center (Trento), we proposed a set-up based on a mixture of two superfluid species of bosonic atoms, where a majority of atoms A (light) are mixed with a minority of atoms B (heavy). The mechanical rotation of the system can be mimicked with a species-selective artificial gauge field, leading to the formation of a vortex lattice for species A. Due to repulsive A/B interactions, B atoms are trapped by vortices of species A, so that they feel an effective triangular-lattice potential, analogous to the one which is generated through optical lattices (see below). The behavior of B atoms is then captured through an effective Bose-Hubbard model. If one also considers the Tkachenko excitations of the lattice, two additional terms appears in the effective model: A long-range attraction and a density-dependent hopping. We studied the phase diagram as a function of the microscopic parameters of the mixture (through variational ansätze and quantum Monte Carlo calculations), and determined how each term modifies the Mott-insulator lobes.

      See:

      Bose-Hubbard models in optical lattices

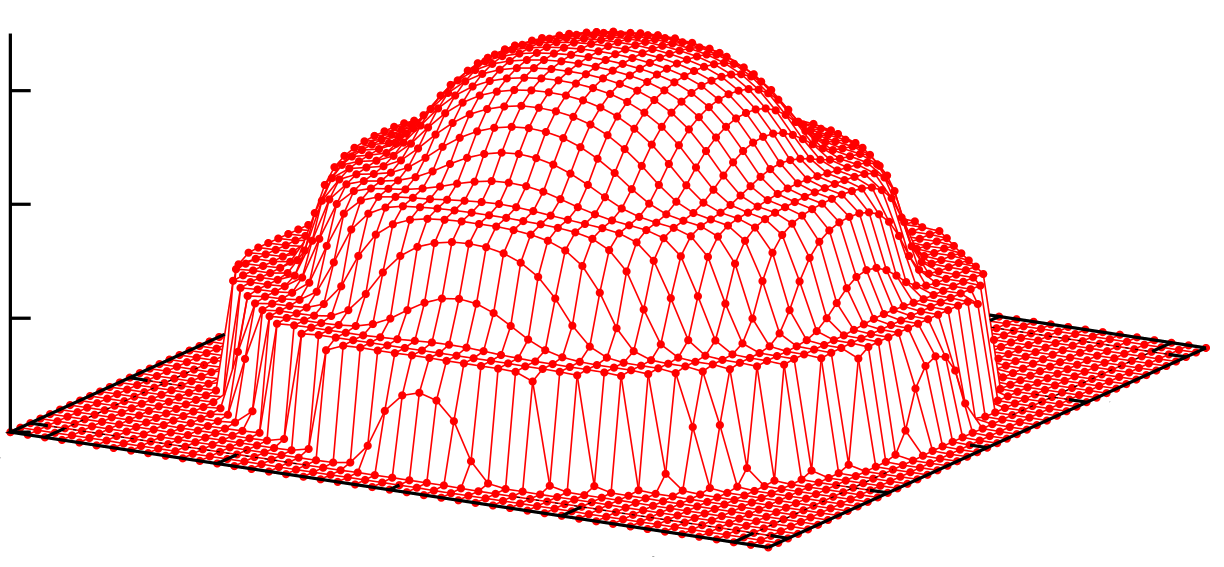      Wedding-cake structure Optical lattices potentials are often used to trap cold atoms in an artificial lattice generated by laser beams. We focus on bosonic atoms, which in this setup show a quantum phase transition between the superfluid and Mott-insulator phases. In typical realization, an additional external potential is used to confine the atomic cloud. This leads to an inhomogeneous "wedding-cake" structure, made by alternating shells of the two different phases. Upon increasing the interatomic on-site repulsion, new Mott-insulator domains form, as signaled in the visibility of the momentum distribution. This is visible in the experiments realized by our collaborators at the Institut für Laserphysik (Hamburg). The Gutzwiller ansatz, adapted to the inhomogeneous case, is not sufficient to capture the position of these features, while more precise quantum Monte Carlo calculations (although based on the Local Density Approximation) provide a better match with the experimental data.
      Within the same framework, we address the Bose-Hubbard model on a two-dimensional bipartite lattice, where the sites on two sublattices A and B (disposed as in a checkerboard) have different depths. The coherence of the system is measured as a function of the lattice depth and the energy difference between the two sublattices. We use a generalized Gutzwiller ansatz for this model to interpret the experimental results. We find that when the energy difference between the two sublattices is large, sublattice B is emptied and atoms form a Mott-insulating phase for the effective model which only includes sites A. Moreover, perturbation-theory prediction can be well fitted to the experimental data in the limit of weak hopping parameter.

      See:
      • M. Liberto, T. Comparin , T. Kock, M. Ölsclhäger, A. Hemmerich, C. Morais Smith, Controlling coherence via tuning of the population imbalance in a bipartite optical lattice, Nat. Commun. 5, 5735 (2014) [arXiv:1412.4040].
      • T. Comparin, Numerical study of trapped and extended Bose-Hubbard models (MSc thesis, 2013), pdf.

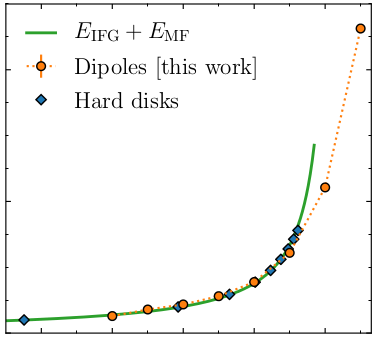
      Classical three-body hard-core model

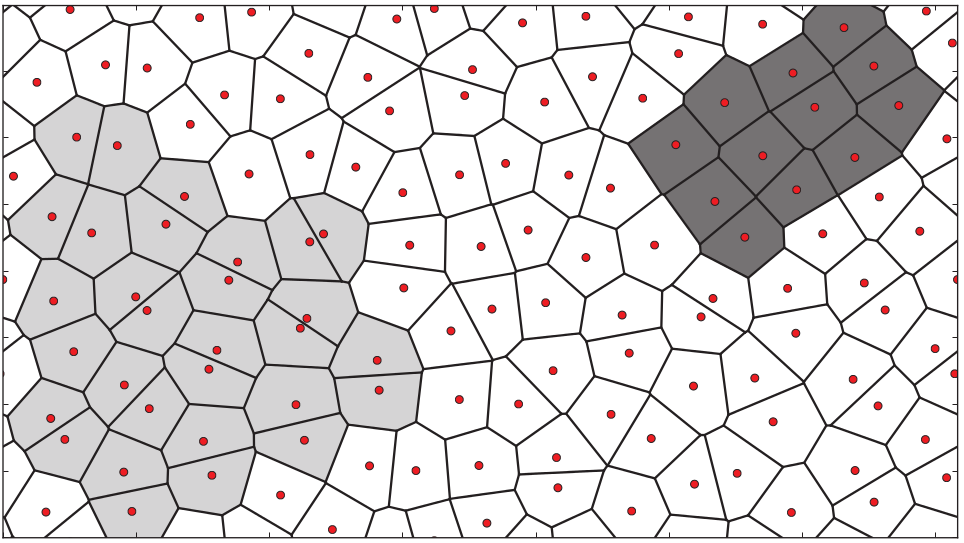      Three-body-cutoff model Hard disks and hard spheres are central models in Statistical Mechanics, and also some of the first ones to be treated by numerical methods as Monte Carlo or Molecular Dynamics. In a recent study of the unitary Bose gas in our group, the model of choice includes a hard cut-off on the three-body distance (that is, the root-mean-square distance of a triplet of particles). We push this model to the regime of large temperature and large density, and study the classical system which only includes a three-body hard-core potential (to be compared with the usual pairwise hard-core repulsion). For this generalized model, in two and three dimensions, we find a liquid-solid phase transition upon increasing pressure. Three-body interactions give rise to peculiar structures in the limit of infinite pressure: A triangular lattice of dimers in two dimensions, and a simple-hexagonal lattice of single particles in three dimensions. Starting from these infinite-pressure structures (also found through simulated annealing), we used Monte Carlo simulations in the fixed-pressure ensemble to measure the phase diagram. The two-dimensional solid is particularly interesting, since the dimer-dimer effective interaction can be seen at the same time as a frustrated spin-spin coupling (concerning the dimers' orientation) or as a hard-disk repulsion (concerning the dimers' positions).

      See:
      • T. Comparin, S. C. Kapfer, W. Krauth. Liquid-solid transitions in the three-body hard-core model, EPL 109 (2015), 20003 [arXiv:1410.1454].
      • T. Comparin, From few-body atomic physics to many-body statistical physics: The unitary Bose gas and the three-body hard-core model (PhD thesis, 2016), pdf.